Designing a Leaderboard System

Designing a Leaderboard System
Hey there!
My name is Justin LeFebvre and I’m a Senior Platform Engineer here at Beamable. My job is to primarily design, implement and maintain many of the backend services our product will be providing to enthusiastic game makers like yourself.
Today, I would like to talk with you about how I went about designing our leaderboard ranked scoring algorithm.
Why should you care about leaderboard design?
Imagine you are trying to create the world’s best competitive multiplayer mobile game. As an avid gamer, you are undoubtedly familiar with the many excellent examples we have today. Games such as, Clash of Clans, Clash Royale, and Vainglory all have one thing in common. Very specifically, all of these games drive player engagement through the use of competitive leaderboards which assign players a rating relative to their opponents which changes over time. These ratings can also be used to drive effective and fair matchmaking, thus allowing your players to play against opponents of similar skill. Given that, you realize that your game will definitely need this feature but this begs the question, how would you go about writing this sort of thing? Fortunately for you, we at Beamable have already put in the legwork and would like to show you what we do.
A generalized leaderboard algorithm for you!
Some of the questions we will answer today are:
- If given a set of players of varying skill levels, is it possible to assign each of them a numerical score which will reflect their overall skill relative to each other?
- Is it possible to generalize the algorithm to determine that score to games of greater than 2 opposing sides?
I’m pretty happy to report that, through a bit of research and experimentation, I have come up with something that should work pretty well for most game makers out-of-the-box with some knobs to turn to tailor the solution to your specific game.
Typical options for tracking player ratings
Traditionally, when a game maker wants to implement a ranking system for his/her players, he/she typically has 3 options available.
Option 1: Implement Microsoft’s Trueskill(tm) algorithm or a variant.
Option 2: Implement the Elo algorithm or a variant.
Option 3: Write a custom algorithm.
While each option has its merits, for our leaderboards, I’ve chosen to go with a slight variant on Option 2 which accounts for games of greater than 2 opposing factions.
Writing the leaderboard algorithm
So, given that we’re providing an implementation of Elo’s algorithm, what is it? The crux of the math around how Elo actually works revolves around the following calculation provided here with little context!

(As an aside, this is actually a Python translation of the code we run in production since we use Scala as our production language for most of our services)
So what does this little Python function do for us? Essentially, this function is a direct translation of the expected score logistic function for the player represented by rating1 given the rating of the player he/she is playing against. Likewise, we should see the expected rating of the other player to be the inverse of the first player’s expected rating.

This score is crucial for scaling the amount of points granted to the winning player as well as the amount of points we should remove from the losing player. For example, if a higher rated player beats a lower rated one, we would expect that the players’ ratings relative to each other are “about correct” so the change to each should be minimal. However, if the lower rated player wins, we definitely want to bump that player’s rating higher and more drastically to reflect the fact that this player may actually be better at the game than the one with the current higher rating. Fortunately, this is exactly what our score function gets us.
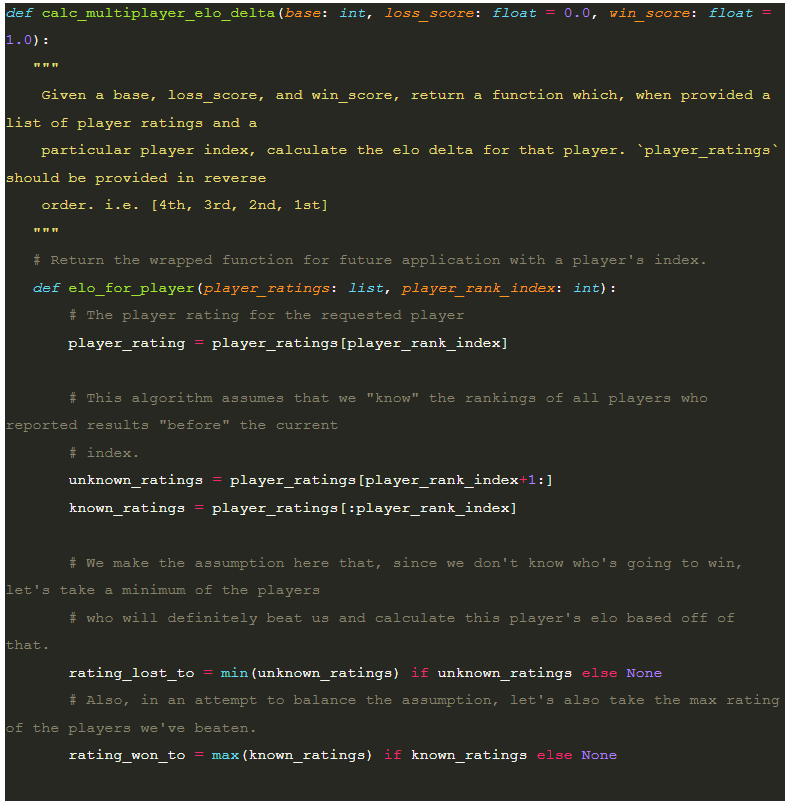
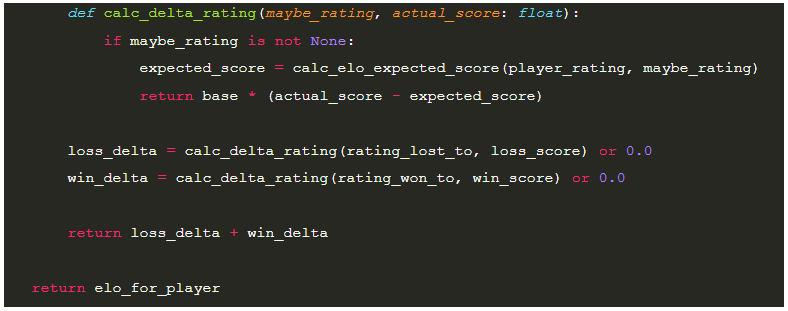
Now that we have the player’s expected score based on the other player’s rating, what can we do with it? In order to calculate the necessary change to each player’s score, we use the following equation where `base` is configurable and `actual_score` will be 1.0 for wins and 0.0 for losses. For our test cases later on, we’ll assume a base of 30.

Now here’s the fun part. Elo, on its own, is an excellent way of determining player ratings for 1 v 1 matches but what do we do when we have a game that is a 4 or more person free-for-all? What’s even more interesting is that, due the mechanics of a free-for-all game, it likely means that at the time you want to calculate the rating for a particular player, the game itself may not actually be over yet. Therefore, it isn’t possible or desirable to get the full results of the match for all players at the time you wish to calculate the new ratings. More specifically, while calculating the score for each player, the results of players who did worse than the current player are known but anyone who did better will specifically not be known until the game is fully over.
Given that level of uncertainty, we will be updating our leaderboards with the following heuristic. For each player in the match, we will be calculating a delta against the player in the “unknown” set of rankings (players who beat us) with the minimum rating. Likewise, for balance, we will be calculating a delta against the player in the “known” set rankings (players we beat) with the maximum rating. This allows us to come up with a way to approximate the delta change to the ratings in a way that behaves similarly to if each player played 2 matches instead of 1.
Here’s the code for that:
Ensuring the accuracy of the leaderboard algorithm
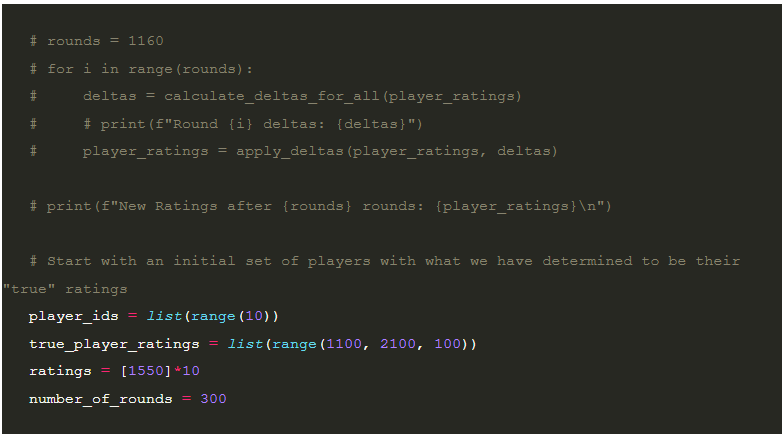
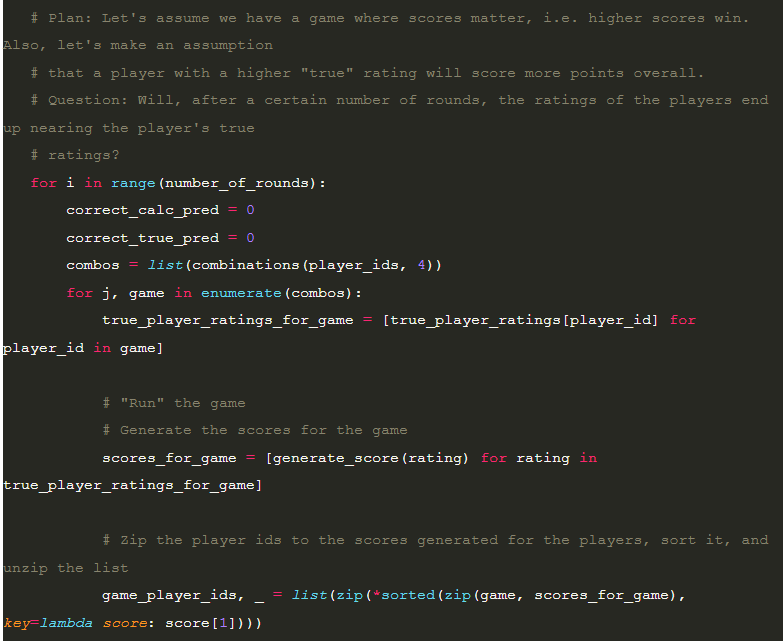
Now that we have this fancy function to calculate the Elo delta for players, and a general method for updating player ratings, how can we go about testing that the algorithm is working as expected? For that, I applied a very similar strategy to this post by Tom Kerrigan. The idea is that you generate a list of “true” ratings for players to simulate having a number of players at different skill levels. The purpose of these ratings is to use them as a seed to generate a simulated score with some amount of “reasonable” deviation.

I then created a list of “base” ratings which I default to the midpoint of the “true” ratings as the initial condition to run the simulation. This allows me to test if the algorithm’s updates to the ratings are increasing the predictive ability of the ratings to determine the outcome of any individual match. I, then, enumerate the list of 4 player combinations of players to run game simulations. The theory is, if I can use the “true” ratings as a reasonable predictor for the outcome of the games, then after some N simulations, the updated ratings should be similarly predictive.
Here’s that code.

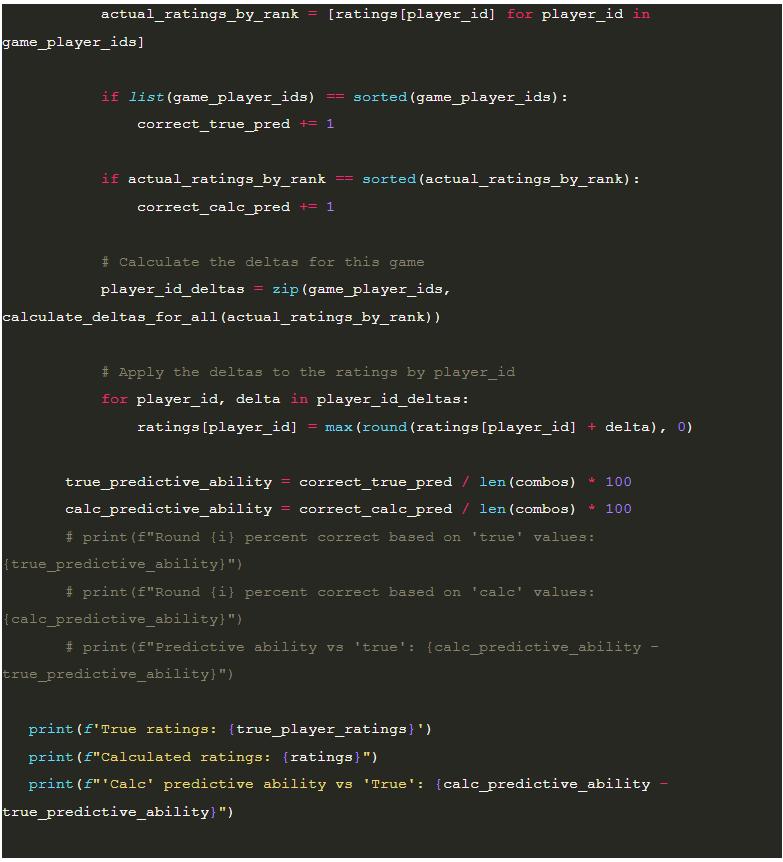
What’s interesting here is that if I run the code with a simulation size of 1 we end up with something around a 1% to 5% deficit in the ability to predict the outcome of any particular game.

However, when running the simulation 10 times we see that the deficit in predictive ability is all but reclaimed with the results being < .5% and often 0.

Now you may be asking yourself, but wait! Why are the calculated ratings for the lower players so much lower than their “true” ratings. The reason for that is mostly because the “true” ratings are merely just used to seed the scores being generated per game simulation. In this particular run, the “1100” ranked player actually had a string of rough luck and based on the way we’re generating the scores ends up doing more poorly in general. That said, the only thing we really care about, however, is whether or not a player who is generally “worse” is ranked lower than a player who is generally “better” and as you can see, this algorithm achieves that.
Last thing to note, if the deviation of the scores is greater, e.g. +-300 rather than +-200, we can observe that the scores are generally closer to where we’d expect them to be but the predictive ability is less accurate compared to the “true” ratings because the results of each individual match are more varied for the 2nd and 3rd spots.
I appreciate you making it this far and hope that you learned something. Please feel free to leave your comments and feedback!
In the next installment, we’ll be talking about how you can use Beamable to implement this in your own games!




